New system classifies materials according to spin and charge Hall conductivity
Researchers from the Theory Department of the Max Planck Institute for the Structure and Dynamics of Matter (MPSD) at the Center for Free-Electron Laser Science (CFEL) in Hamburg and UNIST (Ulsan National Institute of Science and Technology) in Korea used a state-of-the-art quantum dynamical method to calculate the quantum of spin or charge Hall conductivity, by which they successfully classified intrinsic topological natures of materials. Their work has been published in PNAS.
Einstein is commonly quoted as saying: "The most incomprehensible thing about the world is that it is comprehensible. The fact that it is comprehensible is a miracle.” This statement is derived from an article he wrote in 1936 for the Journal of the Franklin Institute. From a physicist’s perspective, such a ‘miraculous comprehension’ most likely indicates that the observed phenomena are very well interpreted by the natural laws, expressed as mathematical equations.
On the other hand, the objectivity and indispensability of mathematical knowledge have been debated ever since Plato and Aristotle. Similarly, questions regarding the role of mathematics in the study of physical phenomena have been raised in recent solid state physics, particularly on the topological notion of insulators. Thouless et. al. proposed in 19821 that the Hall conductivity of an insulator is to be quantized as indexed by a mathematically-devised integer, reflecting the topological structure of the quantum mechanical nature.
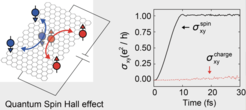
Since then, Michael Berry (1984)2 has identified that such a mathematical number should be related to the phase structure of the quantum mechanical wave-function. According to Haldane (1988)3 and Kane and Mele (2005)4, real materials can be geared by spin-orbit coupling to possess such a non-trivial topological number. This has resulted in a wealth of studies to explore topologically non-trivial materials, particularly for the systems preserving time-reversal symmetry.
In this very mathematical characterization of physical systems, a great doubt is cast over the realness of the mathematically devised number or whether the topological constant can be measured experimentally. Instead of directly contemplating on this issue, the team has developed a computation method that can accurately calculate the Hall conductivity of insulators.
The scientists found that the entire classification of these materials can be achieved by their conductivity itself instead of the mathematically devised topological number. By calculating the time-dependent quantum mechanical equation, they were able to numerically quantify the electrons’ velocity, which was formulated by Michael Berry (1984). The summation of the electrons’ velocity is to be quantized and the detailed intrinsic quantum mechanical structure can be labelled by those quantum numbers.
In short, the team proposes to use physical quantity, less contaminated by mathematical notion, to characterize the materials’ properties, which provide a more direct link to experimental measurements.
REFERENCES
1 D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Quantized Hall Conductance in a Two-Dimensional Periodic Potential, Physics Review Letters 49, 405 (1982)
2 M. V. Berry, Quantal Phase-Factors Accompanying Adiabatic Changes, Proc. R. Soc. Lon. Ser-A 392, 45 (1984).
3 F. D. M. Haldane, Model for a Quantum Hall-Effect without Landau-Levels-Condensed-Matter Realization of the Parity Anomaly, Physical Review Letters 61, 2015 (1988)
4 C. L. Kane and E. J. Mele, Quantum spin Hall effect in graphene, Physical Review Letters 95, 22 (2005)












