
Quantum many-body systems in nonequilibrium
In many cases, the complex properties of strongly interacting lattice systems cannot be catptured by density functional theory or static mean field theory. In equilibrium, dynamical mean-field theory (DMFT) has become a standard approach to overcome this problem. DMFT is used for the ab-initio description of correlated materials, and its cluster extensions can capture the effect of short range correlations which are important in low-dimensional systems such as the high Tc cuprates. In our group we develop generalizations of these techniques, based on their reformulation within the framework of Keldysh Greens functions, to describe the real-time dynamics of correlated systems. For more information:
- H. Aoki, N. Tsuji, M. Eckstein, M. Kollar, T. Oka, Ph. Werner, Reviews of Modern Physics 86, 779 (2014)
Quantum Impurity models

Within (cluster) DMFT, lattice models such as the Hubbard model are mapped to an impurity model in which a single site or cluster is embedded in a bath of noninteracting degrees of freedom. In addition to its role within DMFT, the nonequilibrium dynamics of these impurity models is interesting in its own right, e.g., for the description of non-linear transport through quantum dots. To solve these models, we use and develop several complementary numerical approaches:
- Real-time quantum Monte Carlo can give numerically unbiased results for short times, but is limited by the dynamical sign problem.
- A systematic strong coupling expansion becomes exact for a lattice of isolated atoms and is thus valuable for investigating the Mott phase [Eckstein and Werner, Physical Review B 82, 115115 (2010)]. Recent generalizations of this approach involve electron-phonon systems [Werner and Eckstein, Physical Review B 88, 165108 (2013)], multi-orbital extensions [Eckstein and Werner, arxiv:1410.3956], and bosonic systems [Strand, Eckstein, and Werner, Physical Review X, 5, 011038 (2015)].
- To develop techniques that do not rely on either weak or strong coupling, one can start from a representation of the impurity problem by a time-dependent Hamiltonian [Gramsch, Balzer, Eckstein, and Kollar, Physical Review B 88, 235106 (2013)]. This allows one to use wave-function based numerical techniques, such such as multiconfigurational time-dependent Hartree [Balzer, Li, Vendrell, and Eckstein, Physical Review B, 91, 045136 (2014)]. Particularly promising in this context is the time-dependent density matrix-renormalization group (tDMRG); for a recent application, see [Balzer, Wolf, McCulloch, Werner, and Eckstein, arxiv:1504.02461].
Kadanoff-Baym equation
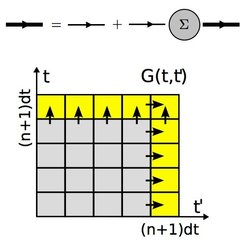
A long-time goal of our research is to arrive at an ab-initio approach to the real-time dynamics of lattice systems, as equilibrium DMFT is nowadays for the study of equilibrium properties. This requires one to solve equations of motions for Keldysh Green's functions of multi-band systems. The numerical bottleneck is that these so-called Kadanoff-Baym (KB) equations, require a memory integration over all previous times. Finding possible ways to overcome this limit [see, e.g., Balzer and Eckstein Physical Review B 89, 035148 (2014)], and the development of a versatile code-package for solving the KB equations is a part of our research.

