Materialeigenschaften lassen sich durch Elektronengeschwindigkeit beschreiben
Wissenschaftler der Theorieabteilung des MPSD am Center for Free-Electron Laser Science (CFEL) in Hamburg und Ulsan National Institute of Science and Technology (UNIST) in Korea haben eine moderne quantenmechanische Methode benutzt, um Spin- und Ladungsstrom zu berechnen und dadurch die inneren topologischen Strukturen von Festkörpermaterialien zu klassifizieren. Diese Arbeit wird in PNAS veröffentlicht.
Wie Albert Einstein 1936 im Journal of the Franklin Institute schrieb: “Das ewig Unbegreifliche an der Welt ist ihre Begreiflichkeit.“ Aus Sicht der Physik bedeutet dieses “wundersame Begreifen” meistens, dass die beobachteten Phänomene sich anhand der bekannten Naturgesetze durch mathematische Gleichungen erklären lassen.
Andererseits werden sowohl die Notwendigkeit als auch die Objektivität der mathematischen Sprache schon seit Platon und Aristoteles diskutiert. Genau solche Fragen zur Rolle rein mathematischer Formulierungen für die Erforschung physikalischer Phänomene beschäftigen auch die moderne Festkörperphysik, insbesondere in der Charakterisierung der topologischen Eigenschaften von bestimmten nichtleitenden Materialien.
Thouless et. al.1 haben 1982 die Quantizierung des Hall-Stroms vorhergesagt, insbesondere dass sie mit einer mathematisch hergeleiteten ganzen Zahl (also 1, 2, 3 usw.) beschrieben werden kann, die auf der topologischen Struktur der quantenmechanischen Zustände des Materials basiert.
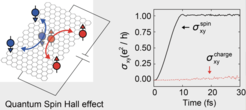
Exakt entgegengesetzter transversaler Fluss von Spin-up und Spin-down Elektronen, so dass es insgesamt keinen Strom von Ladungen gibt. Der Strom des Spins hingegen ist nicht null und kann als eine diskrete (quantizierte) Größe gemessen werden.
Kurz darauf entdeckte Michael Berry (1984)2, dass diese rein mathematische Zahl in einem Zusammenhang mit der Phase der quantenmechanischen Wellenfunktion steht. Später bewiesen Haldane (1988)3 and Kane und Mele (2005)4, dass diese nicht-trivialen typologischen Zahlen in wirklichen Materialien auftreten, wenn in ihren Atomen der Spin der Elektronen mit der Bahn der Elektronen gekoppelt ist.
Diese Charakterisierung von physikalischen Systemen basiert auf rein mathematischen Argumenten. Die Wirklichkeit der typologischen Konstanten, also der erwähnten ganzen Zahlen, zur Klassifizierung von Materialien wird oft bezweifelt, insofern sie überhaupt in einem Experiment beobachtet werden können.
Statt dessen entwickelte das Forschungsteam eine computerbasierte Methode, die den Hall-Strom in nichtleitenden Materialien berechnet. Dabei entdeckten die Wissenschaftler, dass solche Materialien schon durch diesen Strom anstatt der rein mathematisch motivierten typologischen Zahlen klassifiziert werden können.
Durch die Berechnung der zeitabhängigen quantenmechanischen Gleichungen gelang es ihnen, die Geschwindigkeit der Elektronen gemäß Michael Berrys Formulierung zu bestimmen. Wenn diese Geschwindigkeit der Elektronen aufsummiert wird, ergibt sie eine ganze Zahl, mit der man die quantenmechanische Struktur des Materials klassifizieren kann.
So hat das Team gezeigt, dass der Strom, also eine physikalisch messbare Größe, die nicht auf mathematischen Konzepten beruht, verwendet werden kann, um die Eigenschaften von Materialien zu charakterisieren.
REFERENZEN
1 D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Quantized Hall Conductance in a Two-Dimensional Periodic Potential, Physics Review Letters 49, 405 (1982)
2 M. V. Berry, Quantal Phase-Factors Accompanying Adiabatic Changes, Proc. R. Soc. Lon. Ser-A 392, 45 (1984).
3 F. D. M. Haldane, Model for a Quantum Hall-Effect without Landau-Levels-Condensed-Matter Realization of the Parity Anomaly, Physical Review Letters 61, 2015 (1988)
4 C. L. Kane and E. J. Mele, Quantum spin Hall effect in graphene, Physical Review Letters 95, 22 (2005)
